When you grapple with a new idea, where do you start? Most people concentrate on the whole or the parts – either the entity that is the overall idea or the entities that compose it. That we approach ideas in this manner and don’t think about them instead as sets of relationships among components seems to be natural. Relationships, if we get around to them at all, are secondary considerations.
Not everyone acts this way – art critics, as counterexamples, come from a discipline dedicated to critical evaluation and have raised the study of relationships to a high level of importance. But even there, the kinds of relationships examined are specific and tightly focused. For most people, relationships are just not given much attention and even for those who do think about them, the level of involvement is not very high.
This is perplexing considering another familiar human trait. Ask anyone how two items picked at random relate to each other and, after a little thought, they will almost always find multiple relationships – often unconventional and insightful. If anything, once the door is opened, the range of discernible relationships seems almost unlimited.
Considering what we know about how innovation responds to fresh stimulus, it would seem that planners, designers and inventors should be very interested in relationships, at least as much as in the things related!
A Case in Point
Some years ago, I was consulting with a company developing an advanced system for hydrotherapy in the home. A planning team was using Structured Planning to develop a systems concept, and we had reached the stage where we had a number of component ideas being drafted. At the time, I was working on descriptions for a deep tub, some special water jets for muscle stimulation, a chair that swung into the tub to allow a handicapped or elderly bather to enter and leave, and a massage table that would be in a “water room” along with the other equipment as an extensions of bathing and hygiene to a wider realm of health care.
I had just finished the description of the special qualities of the new water jets and was writing the description of the chair when I began thinking of interference problems between the chair, once it was immersed, and the operation of the jets, which were supposed to be able to operate sequentially along the spine and across the neck and shoulders. In an a-ha moment, I thought “Why not put the jets in the chair frame?” The realization that I had changed focus from entity to relationship rose to conscious level, and with the new viewpoint, I saw how the tub could be simplified, how chair functionality could be improved, and how the massage table could be incorporated with the chair as an unfolding pad that fit onto the chair laid flat. The overall concept was more sophisticated, took up less space, and offered greater comfort and functionality for any bather—handicapped or not.
The key was shifting focus from entities to relationships, and then incorporating the new ideas obtained from exploring possible relationships into the descriptions of the entities. A new innovation tool!
The Right Kinds of Relationships
Almost anyone born since the 1940’s has wired-in memories of system diagrams and flow charts. The then new world of systems was expressed as flows of inputs and outputs. The flows might have been material: liquids, electrons, shipments of goods; or information: signals, messages, data; or they might have been steps in a process. Whatever the element transmitted, the relationships almost certainly would have been flows.
Of course, there are many other kinds of relationships. We just don’t think of them as readily. Some show up implicitly, such as “works for” defining an organization chart, and some form bases for purposeful work, such as “evolved from” defining evolutionary taxonomic structures. Both of these are predefined, used analytically to establish links among entities.
In contrast, for those seeking new ideas, the most useful relationships are not predefined. They are revealed from the consideration of entities together. The act of consideration is not one of testing entity pairs for a predefined relationship to establish whether they have it (as an analyst would), but one of examining entity pairings to speculate upon what relationship/s could exist (as an innovator would).
Relationships can be one-way or two-way. An entity can support another (one-way) or two entities can work together in some way (two-way). In the hydrotherapy example (and most cases of innovative use), the “directedness” or “non-directedness” is there, but weakly, not as clearly apparent as for testable analytic relationships. Indeed, the likelihood of finding useful, inventive relationships is greatly increased when an open, less constrained form is encouraged. The possibilities are greatly extended.
Relationships can also be reflexive, a term that means that an entity can be considered with itself. For inventive exploration, that often means expecting that more than one copy of the entities is involved in the system, and relationships between and among them should be pursued. In the hydrotherapy example, considering a water jet with other water jets suggests that jets might be programmed to work in sequences like a masseuse would in applying a massage.
Questions to ask of entities being considered together include, “How should or could entity x work with entity y? What new system feature/s are possible if entity x works with entity y? What new property/ies would make entity x work in a new or better way with entity y?”
When relationships are being explored among entities, it is also a good time to ask a related question, “How strong is the relationship between these two entities?” Knowing something about the strength of associations will be very important in explaining the system, a subject that I will deal with in an upcoming article.
How Many?
In theory, for any system of entities, it would be good to consider all the pairings of entities for possible relationships. In practice, that may be a large number. Basically, it means considering n things against the same n things, or n-squared considerations, actually, the number isn’t so large since, if we really consider all n-squared possibilities, we will be considering almost all possibilities twice. I say almost all, because when we consider an entity against itself, we only do that once. Figure 1 shows all this graphically.
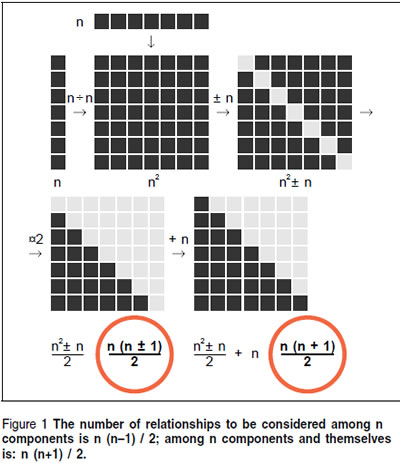 |
At the upper left, the result of preparing for the consideration of n things against themselves produces a matrix n x n. Removing the n cells along the diagonal representing the considerations of entities against themselves (the reflexive case) leaves upper right and lower left halves of the matrix, which clearly shows that considerations will occur twice. Removing half leaves just the cells necessary to cover all comparisons excluding entities against themselves. Adding back the n cells of the diagonal provides all the cells necessary for consideration of every entity with every other entity, including consideration of each entity with itself.
Algebraic equivalents are shown below each graphic step. End results are circled, shown factored to make mental calculation easier. On the left is the calculation for minimum considerations without self-consideration; on the right is the same calculation with self-consideration.
So, for a complex system concept with 50 component entities, the number of considerations to completely explore all possible relationships, including self considerations, would be: (50 x 51) / 2 = 1,275. That’s a lot of work.
Fortunately, there is a useful simplification. Complexity is almost never uniform. A complex concept almost certainly will consist of several subsystems of entities highly associated internally; more sparsely associated elsewhere. And these characteristics usually are extended hierarchically. If the exploration of potential relationships is confined to the subsystems, most of the potentially fruitful possibilities will be explored, and most of the (likely) unproductive considerations will be conveniently avoided.
Considering the 50-component system example again, if it were made up of ten subsystems each with five entities, the number of relationships to be explored for each subsystem would be: (5 x 6) / 2 = 15, and the total for the 50-entity concept would be: 10 x 15 = 150, less than 12% of the 1,275 possible. If the subsystems were only five, with 10 entities each, the number of considerations to be made per subsystem would be: (10 x 11) / 2 = 55 with a total of 5 x 55 = 275, still less than 22% of the 1,275 possible. Either way, that’s a significant saving.
Keeping It Simple
The next step is to make the inventive exploration of relationships as easy as possible while making sure everything that should be considered is considered. Using a form is a good idea because it helps to ensure complete coverage. For readability, it would also help if the form were to fit easily on a laptop screen or standard 8 1/2 x 11 page.
Figure 2 shows such a form as used in Structured Planning. It allows exploration of relationships for four entities with themselves or any other four entities. Entities, in this case, are System Elements, the products of the innovation process in Structured Planning’s Synthesis Phase (for explanation, see my article, Shaping Complex Ideas).
 |
The form shows entries as they might have been made for the hydrotherapy example. Entries demonstrate kinds of relationship description. Drawing directly on the ability of individuals to find relationships between any two entities, the empty cells stimulate thought about what makes or could make the two entities work better together. Corner check-off squares in each cell indicate how strong the relationship is.
With a little more analysis, we can see how to use this simple form to examine relationships among any number of entities. Figure 3A shows the cells of the 4 x 4 form. For four entities, we know that there should be 10 cells [(4 x 5) / 2], and there are; all possibilities are covered. Figure 3B expands the number to eight entities and reveals a problem. The 4 x 4 form is fine for 1-4 against themselves and 5-8 against themselves, but for 1-4 vs 5-8, some of the cells to be considered (2-4 vs 5-7) don’t fit the form; they are upside-down. The problem arises because there are eight, not four, different entities being compared. We need the whole 4 x 4 matrix to cover the 16 possible relationships.
 |
Fortunately, we still have the whole 8 x 8 matrix, even if we don’t want to use all of it. If the upside-down triangular section (2-4 vs 5-7) is reflected across the matrix diagonal, it is the same set of relationships, but now right-side up, able to fit the standard form. This works for any number of entities as shown in Figure 3C. If the Discontinuous numbers don’t matter—they are labels, not quantities. The figure shows that, for ten entities, nine forms are necessary to examine all the relationships, including reflexive ones. Three forms will be full 4 x 4’s using all 10 cells; one will be 3 x 3 not using the four cells along the diagonal (as above and shown in Figure 3B), two will be truncated 3 x 3’s (because the number of entities is not a multiple of 4), and three will be truncated 4 x 4’s.

















